DreamCalc is able to solve polynomials of the form:
axn + bxn-1 + cxn-2 ... = 0
where n specifies the order of the polynomial, and may be any value between 2 (quadratic) and 20.
Use the [POLY] key to access the built-in polynomial solver.
When you press the [POLY] key, it will prompt you for the required input, beginning with the order n. The letters a, b, c etc. designate the coefficients which are entered in sequence by pressing [POLY] or [ENTER] to progress to the next one.
The polynomial will be solved once all the coefficients are entered, and you may continue to page through the solutions using [POLY] or [ENTER].
The [STO] key may be used at anytime to hold solutions in memory for use outside the polynomial solver.
Example: Find the solutions to the cubic equation, x3 + 5x2 - 29x - 105 = 0.
[POLY] (Initiates the polynomial solver) 3 [ENTER] (Enter order 3) 1 [ENTER] (Enter coefficients in sequence) 5 [ENTER] -29 [ENTER] -105 [ENTER]
At this point, the solutions will be given in sequence: +5, -3, and -7. You may press [ENTER] to page through them. The solutions will be also be displayed in the Paper Roll Window.
In the above example, all the solutions were real values. In the general case, however, solutions may be complex. In addition, you may input complex coefficients using the [;] key as the separator between real and imaginary components. Complex values are used in the polynomial solver irrespective of whether complex numbers are enabled or disabled in DreamCalc.
When displaying the results, real solutions will be shown first, otherwise the results are unsorted.
As a demonstration, two polynomial plots are presented below which were created with DreamCalc's Function Graph.
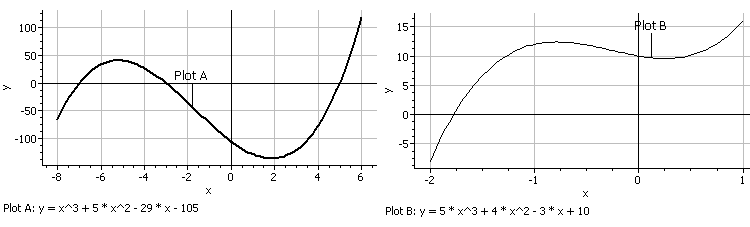
Cubics with Real & Complex Solutions
The first (plot A) shows the cubic example given above, where all the solutions are real. You can see that it crosses the x-axis at the three solution points: +5, -3, and -7. The second (plot B) shows a cubic for which only one real solution exists. Correspondingly, the x-axis is crossed in one place only.
See also: Complex Number Calculations
